Probablistic Technology
Probabilistic Methods
In general, current methods of structural reliability tend to fall into one of five categories: Simulation Methods, Reliability Methods, Importance Sampling Methods, Response Surface Methods, and Perturbation Method.
Simulation Methods
There are several methods in this category, from which Monte Carlo Simulation, Latin Hypercube, and Directional Simulation are considered the most popular ones. In Monte Carlo Simulation deterministic analysis is carried out for a series of sample points (a set of random variables) generated in accordance with their probability distributions. The desired statistics of the response quantities, such as the mean, variance and probabilities, are then evaluated based on the generated samples. The Monte Carlo Simulation has the advantage that it is adoptable to all kind of problems and results can be obtained to the desired accuracy. However, for practical applications, where that usually have very large reliability, this procedure is computationally too intensive, because a large number of solutions are needed to obtain reliable results. However, for practical problems with small probabilities, this approach is usually computationally too intensive since a large number of solutions are needed to obtain reliable results. Other popular methods in this category includes Latin Hypercube and Directional Simulation.
Reliability Methods
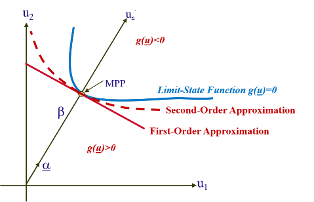
These methods aim at calculating probabilities of structures by replacing the limit-state surface (a boundary between acceptable and unacceptable domains) with a polynomial approximation of the limit-state function, g, about some point on the failure boundary. This point is normally taken as the point nearest to the origin in a transformed standard normal space and is usually referred to as design point, maximum likelihood, or most probable point (MPP). The key to efficient probabilistic analysis is the ability to identify one or more MPPs quickly. The problem is one of constrained optimization, and algorithms for its solution have been extensively investigated. However, it has been recognized that, for some cases, the optimization procedures may require a large number of limit-state function calculations or may lead to erroneous solutions. In terms of practical probabilistic analysis, the problem is magnified even more. PredictionProbe has overcome these shortcomings by developing numerous optimization procedures for practical applications for many special circumstances that ensures accuracy and efficiencies.
Importance Sampling Methods
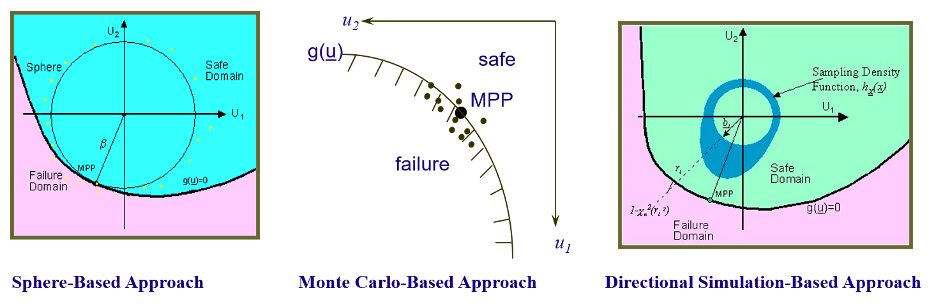
The main problem with simulation methods are that when the failure probability is small, most of the simulation points are not in the failure domain (i.e., are not hits). One technique to increase the number of hits is to bias the choice of the random vector by using a sampling distribution h(x) (called importance sampling distribution) which has more samples in the failure region. In such an approach, once h(x) is defined, N samples of the random vectors are generated from h(x) and for each sample a limit-state function is computed. The failure probability is then estimated using a scale factor to correct for the bias in the sampling distribution in conjunction with the equations defined for mean and standard deviation of failure probability (in Simulation Methods Section). These techniques are categorized as Importance Sampling Methods. The popular Importance Sampling Methods includes: Monte Carlo-Based , Sphere-Based, and Directional Simulation-Based Importance Sampling techniques.
Response Surface Methods
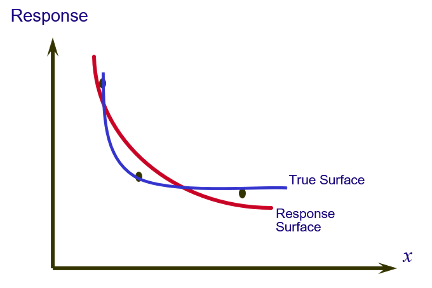
These methods performs probabilistic analysis by replacing and using the response model (or the limit-state function) with its approximation called “response surface.” The analysis is then performed using an appropriate method (e.g., Simulation Methods, Reliability Methods,etc.) without having to utilize the actual response model (or the limit-state function). This approach is particularly useful when the response model (or the limit-state functions) is algorithmic in form (e.g., requires input from another software) and its gradient, which is necessary in Reliability Methods, is difficult to compute. To construct the response surface, one typically computes the response model (or the limit-state function) at a number of points (experiment points) and then fits the response surface to the points by least square method. One important consideration in using response surface methodology is the selection of the “experiment” points. There a number of standard experiment plans for this purpose.
Perturbation Method
The perturbation method involves first- or second-order Taylor series expansion of predictive models around the mean values of the random variables. In thess methods, random variables are characterized by the first and second statistical moments. No distribution information is required. The aim of this method is to compute the first and second moments of the response quantities. The perturbation methods have the advantage that they can be applied to a large variety of problems. However, these methods yield satisfactory results only when the variations of the random variables are small. Another problem associated with this method is the lack of invariance to mechanically equivalent restatements of the limit-state function. Furthermore, since the mean point is likely to be well within the safe region, considerable errors in approximating the failure probability are expected.