Modeling

Types of Models

Typically, various types of models may exist for the same system, entity, phenomena, or process. A conceptual model is the collection of abstractions, assumptions, and descriptions of physical processes representing the behavior of the reality of interest from which the mathematical model or validation experiments can be constructed (adapted from ASME V&V 10). A mathematical model is the collection of equations, boundary values, initial conditions, data needed to describe the conceptual model (ASME V&V 10). The computational model is the numerical representation of the mathematical model for implementation on some computational platform, i.e., a computer program. A simulation is the imitation of the characteristics of a system, entity, phenomena, or process using a computational model. That is, a simulation is the results of an execution of the computational model.

Verification and Validation

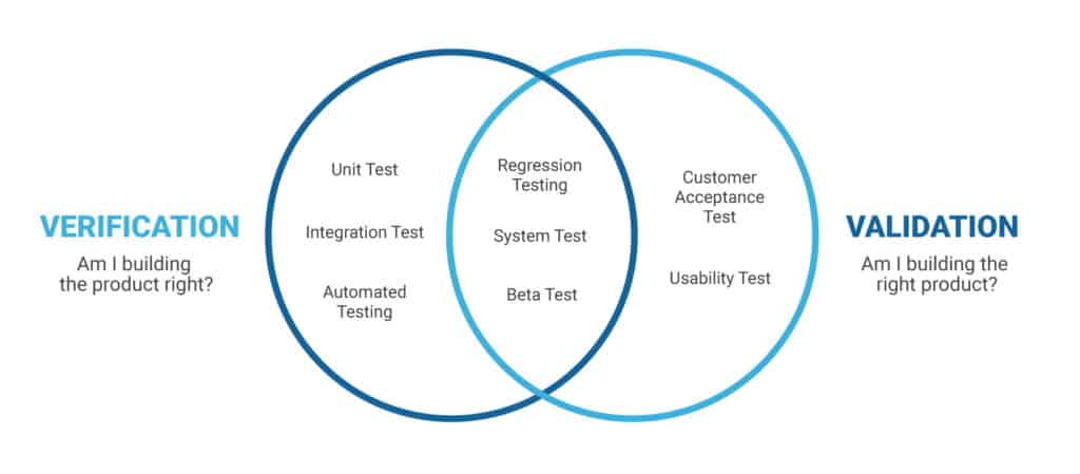
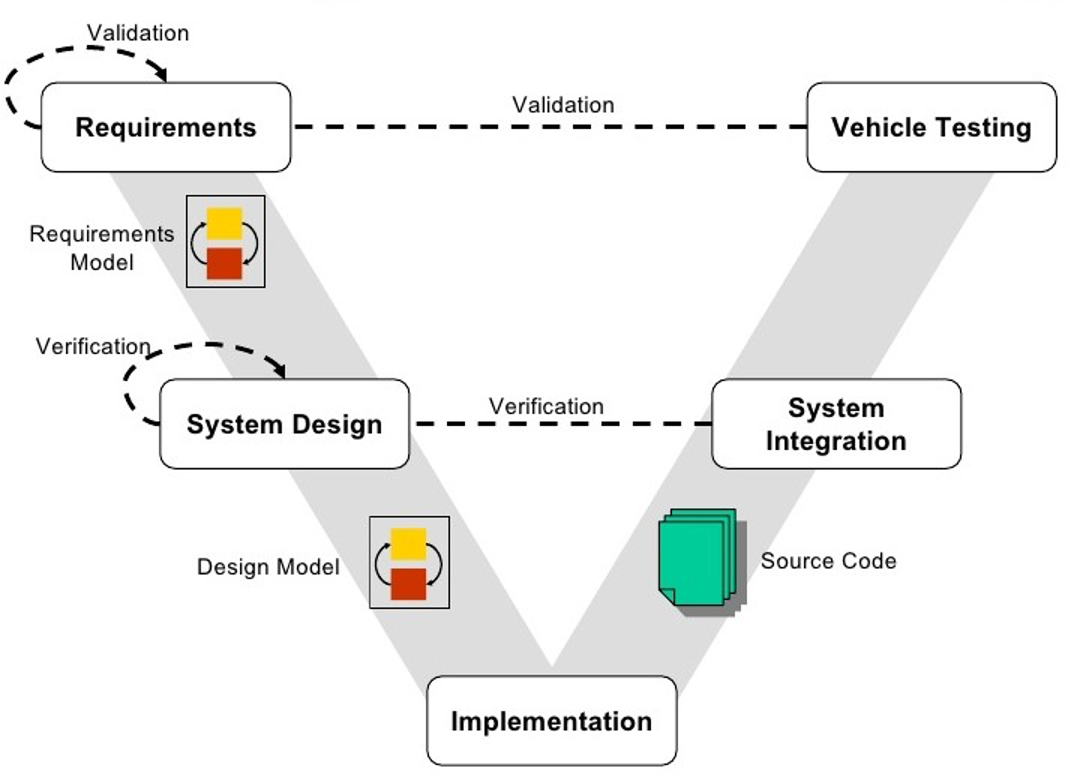
Each of the above models must be verified for correctness and the resulting simulation is also subject to validation. Verification is the process of determining that a computational model accurately represents the underlying mathematical model and its solution from the perspective of the intended uses. Validation is the process of determining the degree to which a model or a simulation is an accurate representation of the real world from the perspective of the intended uses of the model or the simulation. These concepts are illustrated in Figure 1 and Figure 2.

Verification of a deterministic computational model is an extensive and detailed process in which every element of the model must be examined for correctness; ideally this is done iteratively and in parallel with the development of the computational model. Variable types (e.g., integer, float, double precision) must be checked and their usage throughout  program must be consistent; equations and the use of any intrinsic functions must be verified; inputs and outputs must be correct; and finally the use of looping and logical structures must all be verified. In a probabilistic computational model, even many more aspects of the process must be verified for correctness including the types and descriptions of input uncertainty models, the choice of, and inputs to the probabilistic methods must be verified and the use of and implementation of any limit states must be verified.

Validation attempts to quantify the utility of the model for the real-world application. It is preferred (some would say required) that validation be accomplished with a comparison of simulated and actual real-word data (a referent). In many cases, a true referent (actual real-world data) is not available for comparison to the simulation. In this case, one must rely on an iterative validation process in which as many as possible of the building block elements of the simulation are validated and in which also the final simulation result is compared to the best available referents from similar conditions.  This is a process that employs judgment and should likewise employ the wisdom of several Subject Matter Experts to determine the highest quality and relevant sets of data to be used as the referent. Again, in probabilistic computational models, this becomes even more challenging because the probability of infrequently occurring events can generally only be inferred from a probabilistic approach; several different probabilistic implementations of the same problem may be necessary to establish the robustness (and validity) of a given simulation.

Modeling is an Art

Designing and creating accurate and useful models is an art and requires significant experience and skill. The user can rest assured that in all the probabilistic technology examples and applications in which PPI has participated, an extensive amount of verification and validation exercises are performed to assure the accuracy of the models. Given the backgrounds and experience of the PPI team members, verification and validation are primary concerns in delivering reliable products and solutions to our customers.