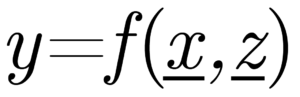Modeling

In general, a predictive model is a mathematical expression relating a dependent variable y, to a set of observable variables x, and a set of unobservable model parameters z.

The predictive model, f(x,z), is usually constructed on the basis of simplifying assumptions using:

• Simplified closed-form physics-based models;
• Analytical physics-based models using sophisticated software tools;
• Empirical models using field data, test results, and/or data produced by analytical physics-based models;
• Process rules; and
• Sometimes on a purely heuristic basis when underlying phenomenon is not well understood.

In addition to inherent uncertainties, which defines random characteristic nature of the observable variables x (e.g., variation in material strength, time to complete a task, price per square foot of residential property in a neighborhood, etc.), there are at least three major phenomena that give rise to uncertainty in a predictive model including:

1. Model Imperfection: This uncertainty is caused by a lack of understanding of the phenomenon and use of simplified mathematical expressions;
2. Measurement Errors: A predictive model is constructed, assessed, verified, and validated based on measured values of the observable variables, which are often in error due to inaccuracies in measurement procedures and/or devices; and
3. Statistical Uncertainty: Statistical uncertainty arises from the inaccuracies associated with lack of adequate data.

The variables models (e.g., wind loads, material properties, time to complete a task, price per square foot of residential property in a neighborhood, speed of a car, etc.) are inherently random, i.e., quantities which are not deterministic and which actually exhibit statistical variations. Furthermore, the mathematical models of an event are invariably imperfect and uncertain. Hence, the future state of an event can only be predicted in probabilistic sense.

The observable variables and unobservable model parameters are characteristically random due to impact of various uncertainties (i.e., quantities that are not deterministic and which actually exhibit statistical variations). The variable models must be constructed statistically using expert knowledge and available data. The process for construction of such models is highly function of data size and costs of producing such data.

PredictionProbe’s systematic, flexible, and scalable processes provide a solid framework for constructing predictive and variable models that will allow analyst to:

• Use one or more combination of physics, statistical data, and process rules;
• Consider expert judgment and subjective information;
• Incorporate various uncertainties;
• Verify and validate the models objectively;
• Minimize the required data; and
• Assess and update the models when new information becomes available.